Mastering Binary Search Trees in Java: A Comprehensive Guide to Insertion, Deletion, and Searching

Binary Search Trees (BSTs) are a fundamental data structure that underpin many algorithms and systems due to their efficient operations for searching, insertion, and deletion. In this comprehensive guide, we'll delve into constructing and managing BSTs using Java. We will explore the intricacies of insertion, deletion, and search operations, while also highlighting real-world applications where these trees are invaluable.

Understanding Binary Search Trees

A Binary Search Tree is a node-based data structure with the following properties:

• Each node contains a unique key (value), a reference to its left child, and a reference to its right child.
• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.

This structure allows for efficient searching, insertion, and deletion operations, typically in O(log n) time complexity if the tree is balanced.

Setting Up Your Environment

Before we dive into coding, ensure you have:

• Java Development Kit (JDK) installed on your machine.
• A preferred Integrated Development Environment (IDE) like IntelliJ IDEA or Eclipse.

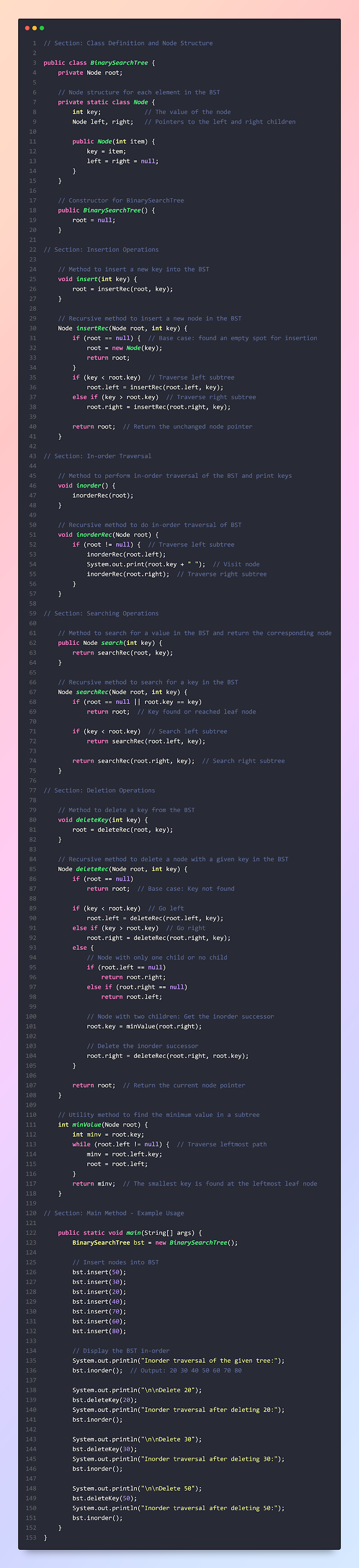
public class BinarySearchTree {
    private Node root;

    // Node structure
    private static class Node {
        int key;
        Node left, right;

        public Node(int item) {
            key = item;
            left = right = null;
        }
    }

    // Constructor for BST
    public BinarySearchTree() {
        root = null;
    }

    // Helper method to insert a new key
    void insert(int key) {
        root = insertRec(root, key);
    }

    // Recursive insertion function
    Node insertRec(Node root, int key) {
        if (root == null) {
            root = new Node(key);
            return root;
        }
        if (key < root.key)
            root.left = insertRec(root.left, key);
        else if (key > root.key)
            root.right = insertRec(root.right, key);

        return root;
    }

    // Helper method to perform in-order traversal
    void inorder() {
        inorderRec(root);
    }

    // Recursive in-order traversal
    void inorderRec(Node root) {
        if (root != null) {
            inorderRec(root.left);
            System.out.print(root.key + " ");
            inorderRec(root.right);
        }
    }
}

Insertion in a Binary Search Tree

Inserting a new node involves finding the correct position for it to maintain the BST properties. The insert method uses recursion to find either an empty spot or to navigate down the tree.

// Insert example usage
BinarySearchTree bst = new BinarySearchTree();
bst.insert(50);
bst.insert(30);
bst.insert(20);
bst.insert(40);
bst.insert(70);
bst.insert(60);
bst.insert(80);

// Display BST in order
bst.inorder(); // Output: 20 30 40 50 60 70 80

Searching for a Value

Searching involves traversing the tree from the root, following left or right children based on comparison with each node's key.

// Method to search for a value in BST
public Node search(int key) {
    return searchRec(root, key);
}

// Recursive search function
Node searchRec(Node root, int key) {
    if (root == null || root.key == key)
        return root;

    if (key < root.key)
        return searchRec(root.left, key);

    return searchRec(root.right, key);
}

Deletion from a Binary Search Tree

Deletion can be more complex and involves three scenarios:

1. Node to be deleted is a leaf: Simply remove the node.
2. Node to be deleted has one child: Replace the node with its child.
3. Node to be deleted has two children: Find the inorder successor (smallest in the right subtree) or predecessor, replace the node's key with that of the successor/predecessor, and delete the successor/predecessor.

// Method for deleting a node
void deleteKey(int key) {
    root = deleteRec(root, key);
}

Node deleteRec(Node root, int key) {
    if (root == null)
        return root;

    if (key < root.key)
        root.left = deleteRec(root.left, key);
    else if (key > root.key)
        root.right = deleteRec(root.right, key);
    else {
        // Node with only one child or no child
        if (root.left == null)
            return root.right;
        else if (root.right == null)
            return root.left;

        // Node with two children: Get the inorder successor
        root.key = minValue(root.right);

        // Delete the inorder successor
        root.right = deleteRec(root.right, root.key);
    }
    
    return root;
}

int minValue(Node root) {
    int minv = root.key;
    while (root.left != null) {
        minv = root.left.key;
        root = root.left;
    }
    return minv;
}

Real-World Applications

Binary Search Trees are widely used in real-world applications such as:

• Database Indexing: Efficiently managing and querying large datasets.
• File Systems: Organizing files based on timestamps or other metadata.
• Symbol Tables: Used by compilers to store information about source program variables.

BSTs provide a balance between simplicity and efficiency, making them ideal for many scenarios where quick search operations are crucial.

Conclusion

By mastering the insertion, deletion, and searching operations in Binary Search Trees using Java, you can significantly optimize your applications. This guide has provided the foundational knowledge required to implement and manage BSTs effectively. With practice, these concepts will become second nature, enabling you to tackle more complex data structures with confidence.